(本小题12分)设 的内角
的内角 的对边分别为
的对边分别为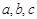 ,满足
,满足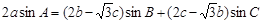 .
.
(1)求角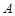 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
(本小题12分)已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数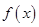 的解析式,并写出
的解析式,并写出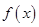 的单调减区间;
的单调减区间;
(2)已知 的内角分别是
的内角分别是 ,角
,角 为锐角,且
为锐角,且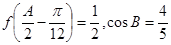 ,求
,求 的值.
的值.
(本小题10分)已知数列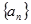 是公比不为
是公比不为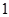 的等比数列,
的等比数列, ,且
,且 成等差数列.
成等差数列.
(1)求数列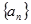 的通项;
的通项;
(2)若数列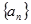 的前
的前 项和为
项和为 ,试求
,试求 的最大值.
的最大值.
(本小题12分)已知函数 .
.
(1)若 =0,判断函数
=0,判断函数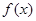 的单调性;
的单调性;
(2)若 时,
时,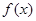 <0恒成立,求
<0恒成立,求 的取值范围.
的取值范围.
(本小题12分)过椭圆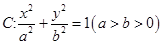 右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
.
(1)求椭圆C的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点P,Q,且 ⊥
⊥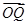 ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.