如图,己知直线l与抛物线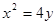 相切于点P(2,1),且与x轴交于点A,定点B(2,0).
相切于点P(2,1),且与x轴交于点A,定点B(2,0).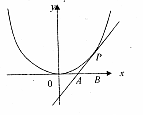
(1)若动点M满足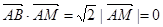 ,求点M轨迹C的方程:
,求点M轨迹C的方程:
(2)若过点B的直线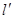 (斜率不为零)与(1)中的轨迹C交于不同的两点E,F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
(斜率不为零)与(1)中的轨迹C交于不同的两点E,F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
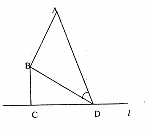
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4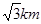 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x>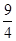 ),点D对跑道AB的视角为
),点D对跑道AB的视角为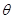 .
.
(1)将tan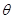 表示为x的函数:
表示为x的函数:
(2)求点D的位置,使得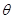 取得最大值.
取得最大值.
如图,已知AC⊥平面CDE,BD//AC,△ECD为等边三角形,F为ED边的中点,CD=BD=2AC=2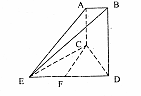
(1)求证:CF∥面ABE;
(2)求证:面ABE⊥平面BDE:
(3)求三棱锥F—ABE的体积。
记数列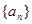 的前n项和
的前n项和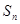 ,且
,且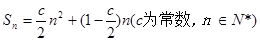 ,且
,且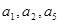 成公比不等于1的等比数列。
成公比不等于1的等比数列。
(1)求c的值;
(2)设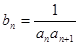 ,求数列{
,求数列{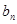 }的前n项和Tn.
}的前n项和Tn.
若关于 的方程
的方程 有实根
有实根
(Ⅰ)求实数 的取值集合
的取值集合
(Ⅱ)若对于 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围