已知梯形ABCD中，AD∥BC，∠ABC =∠BAD =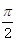
，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE=x，G是BC的中点。沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时，求证：BD⊥EG ；
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x)，求f(x)的最大值；
(3) 当f(x)取得最大值时，求二面角D-BF-C的余弦值.
已知函数
，
．
（I）若函数
在
处取得极值，求的单调区间；
（II）当
时，
恒成立，求
的取值范围．
已知
．
（Ⅰ）若向量
，
，且
∥
，求
的值；
（Ⅱ）在
中，角
的对边分别是
，且满足
，求
的取值范围．
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进行第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品的合格率依次为
，
，
．经过第二次烧制后，甲、乙、丙三件产品的合格率均为
．
(Ⅰ)求第一次烧制后恰有一件产品合格的概率；
(Ⅱ)求经过前后两次烧制后三件产品均合格的概率．
设二次函数
，对任意实数
，有
恒成立；数列
满足
.
（1）求函数
的解析式和值域；
（2）试写出一个区间
，使得当
时，数列在这个区间上是递增数列，并说明理由；
（3）已知
，是否存在非零整数
，使得对任意
，都有
恒成立，若存在，
求之；若不存在，说明理由.
设虚数
满足
为实常数，
，
为实数）.
（1）求
的值；
（2）当
，求所有虚数的实部和；
（3）设虚数对应的向量为
（
为坐标原点），
，如
，求的取值范围.