已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=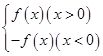
(1)若f(-1)=0,且函数f(x) ≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
等比数列{ }的前n 项和为
}的前n 项和为 ,已知
,已知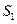 ,
,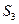 ,
, 成等差数列(1)求{
成等差数列(1)求{ }的公比q;(2)求
}的公比q;(2)求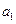 -
- =3,求
=3,求
已知双曲线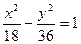 的顶点都是椭圆
的顶点都是椭圆 的顶点,直线
的顶点,直线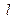 :
: 经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线
经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线 经过椭圆的两个焦点,与直线
经过椭圆的两个焦点,与直线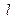 相交于
相交于 、
、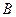 ,试将线段
,试将线段 的长
的长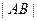 表示为
表示为 的函数.
的函数.
如下的三个图中,右图是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;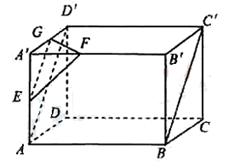
(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结 ,证明:
,证明: ∥面EFG.
∥面EFG.
设函数 ,其中
,其中 (1) 求
(1) 求 的最大值;(2)在
的最大值;(2)在 中,
中, 分别是角
分别是角 的对边,且f(A)=2,a=,b+c=3,求b,c的值
的对边,且f(A)=2,a=,b+c=3,求b,c的值
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.(1)求该总体的平均数; (2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.