已知椭圆 :
: .
.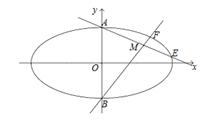
(1)椭圆 的短轴端点分别为
的短轴端点分别为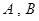 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆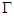 交于
交于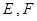 两点,其中点
两点,其中点 满足
满足 ,且
,且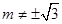 .
.
①证明直线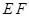 与
与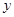 轴交点的位置与
轴交点的位置与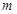 无关;
无关;
②若∆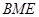 面积是∆
面积是∆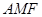 面积的5倍,求
面积的5倍,求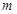 的值;
的值;
(2)若圆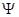 :
: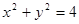 .
. 是过点
是过点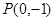 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中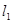 交圆
交圆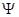 于
于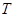 、
、 两点,
两点,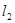 交椭圆
交椭圆 于另一点
于另一点 .求
.求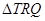 面积取最大值时直线
面积取最大值时直线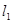 的方程.
的方程.
已知两点A(-1,2)、B(m,3).
(1)求直线AB的方程;
(2)已知实数m∈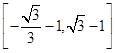 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围.
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:
(1)△ABC中平行于BC边的中位线所在直线的一般式方程和截距式方程;
(2)BC边的中线所在直线的一般式方程,并化为截距式方程.
已知直线l: +4-3m=0.
+4-3m=0.
(1)求证:不论m为何实数,直线l恒过一定点M;
(2)过定点M作一条直线l1,使夹在两坐标轴之间的线段被M点平分,求直线l1的方程.
过点M(0,1)作一条直线,使它被两条直线l1:x-3y+10=0,l2:2x+y-8=0所截得的线段恰好被M点平分.求此直线方程.