大学生自主创业已成为当代潮流。长江学院大三学生夏某今年一月初向银行贷款20000元作开店资金,全部用作批发某种商品,银行贷款的年利率为6%,约定一年后一次还清贷款。已知夏某每月月底获得的利润是该月月初投人资金的15%,每月月底需要交纳个人所得税为该月所获利润的20%,当月房租等其他开支1500元,余款作为资金全部投入批发该商品再经营,如此继续,假定每月月底该商品能全部卖出。
(1)设夏某第 个月月底余
个月月底余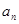 元,第
元,第 个月月底余
个月月底余 元,写出
元,写出 的值并建立
的值并建立 与
与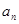 的递推关系式;
的递推关系式;
(2)预计年底夏某还清银行贷款后的纯收入。(参考数据:1.1211≈3.48,1.1212≈3.90,0.1211≈7.43×10﹣11,0.1212≈8.92×10﹣12)
(本小题满分13分)
正数数列{an}的前n项和为Sn,且2.
(1)试求数列{an}的通项公式;
(2)设bn=,{bn}的前n项和为Tn,求证:Tn<.
(本小题满分12分)
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA=a,点O、D分别是AC、PC的中点,OP⊥底面ABC。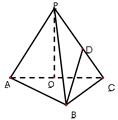
(1)求三棱锥P-ABC的体积;
(2)求异面直线PA与BD所成角余弦值的大小。
(本小题满分12分)
在区间 中随机地取出两个数,求两数之和小于
中随机地取出两个数,求两数之和小于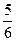 的概率。
的概率。
(本小题满分12分)
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?共有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
(本小题满分12分)
设函数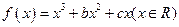 ,已知
,已知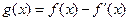 是奇函数。
是奇函数。
(1)求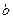 、
、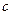 的值。
的值。
(2)求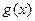 的单调区间与极值。
的单调区间与极值。