已知函数 =
= 。
。
(1)当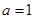 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)求函数 在区间
在区间 上的最小值;
上的最小值;
(3)在(1)的条件下,设 =
= +
+ ,
,
求证: (
(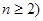 ),参考数据:
),参考数据: 。
。
已知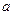 、
、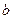 、
、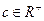 ,
,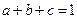 ,求证
,求证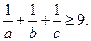
若复数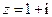 ,求实数
,求实数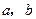 使
使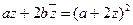 成立.(其中
成立.(其中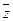 为
为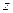 的共轭复数)
的共轭复数)
已知三个函数 ,它们各自的最小值恰好是函数
,它们各自的最小值恰好是函数 的三个零点(其中t是常数,且0<t<1)
的三个零点(其中t是常数,且0<t<1)
(1)求证: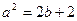
设 的两个极值点分别为
的两个极值点分别为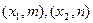 ,若
,若 ,求f(x)
,求f(x)
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度,已知直线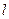 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角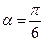
(1)写出直线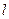 的参数方程;(2)设
的参数方程;(2)设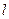 与圆
与圆 相交与A,B,求点P到A,B两点的距离积。
相交与A,B,求点P到A,B两点的距离积。
在对人们的休闲方式的一次调查中,共调查了500人,其中女性250人,男性250人。女性中有50人主要的休闲方式是看电视,另外200人主要的休闲方式是运动;男性中有30人主要的休闲方式是看电视,另外220人主要的休闲方式是运动。
( 1)根据以上数据建立一个2×2的列联表
1)根据以上数据建立一个2×2的列联表
(2)判断性别与休闲方式是否有关系.