如图，△ABC与△CDE均是等腰直角三角形，∠ACB∠DCE-优题课

某中学为了了解本校学生对排球、篮球、毽球、羽毛球和跳绳五项“大课间”活动的喜欢情况，随机抽查了部分学生进行问卷调查（每名学生只选择一项），将调查结果整理并绘制成如图所示不完整的统计图表．请结合统计图表答案下列问题：

抽样调查学生喜欢大课间活动人数的统计表

项目	人数
$A$ 排球	6
$B$ 篮球	$m$
$C$ 毽球	10
$D$ 羽毛球	4
$E$ 跳绳	18

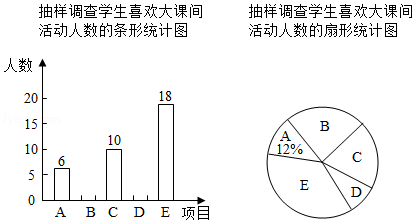
（1）本次抽样调查的学生有　50　人，请补全条形统计图；

（2）求扇形统计图中，喜欢毽球活动的学生人数所对应圆心角的度数；

（3）全校有学生1800人，估计全校喜欢跳绳活动的学生人数是多少？

在 $ΔABC$ 中， $AB = AC$ ， $BC = 6$ ， $S_{ΔABC} = 6$ ．以 $BC$ 为边作周长为18的矩形 $BCDE$ ， $M$ ， $N$ 分别为 $AC$ ， $CD$ 的中点，连接 $MN$ ．请你画出图形，并直接写出线段 $MN$ 的长．

如图，抛物线 $y = x^{2} + bx + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，抛物线的顶点为 $P$ ．已知 $B (1, 0)$ ， $C (0, - 3)$ ．请答案下列问题：

（1）求抛物线的解析式，并直接写出点 $P$ 的坐标；

（2）抛物线的对称轴与 $x$ 轴交于点 $E$ ，连接 $AP$ ， $AP$ 的垂直平分线交直线 $PE$ 于点 $M$ ，则线段 $EM$ 的长为　 $\frac{3}{2}$ 　．

注：抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 的对称轴是直线 $x = - \frac{b}{2 a}$ ，顶点坐标是 $(- \frac{b}{2 a}$ ， $\frac{4 ac - b^{2}}{4 a})$ ．

先化简，再求值： $(1 - \frac{4}{x^{2}}) \div \frac{x^{2} - 2 x}{x^{2}}$ ，其中 $x = - \tan 45 °$ ．

如图，在平面直角坐标系中，四边形 $OABC$ 的边 $OC$ 在 $x$ 轴上， $OA$ 在 $y$ 轴上． $O$ 为坐标原点， $AB / / OC$ ，线段 $OA$ ， $AB$ 的长分别是方程 $x^{2} - 9 x + 20 = 0$ 的两个根 $(OA < AB)$ ， $\tan ∠ OCB = \frac{4}{3}$ ．

（1）求点 $B$ ， $C$ 的坐标；

（2） $P$ 为 $OA$ 上一点， $Q$ 为 $OC$ 上一点， $OQ = 5$ ，将 $ΔPOQ$ 翻折，使点 $O$ 落在 $AB$ 上的点 $O'$ 处，双曲线 $y = \frac{k}{x}$ 的一个分支过点 $O'$ ．求 $k$ 的值；

（3）在（2）的条件下， $M$ 为坐标轴上一点，在平面内是否存在点 $N$ ，使以 $O'$ ， $Q$ ， $M$ ， $N$ 为顶点四边形为矩形？若存在，请直接写出点 $N$ 的坐标；若不存在，请说明理由．