2013年12月21日上午10时，省会首次启动重污染天气Ⅱ级应急响应，正式实施机车尾号限行，当天某报社为了解公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：
（1）完成被调查人员的频率分布直方图；
（2）若从年龄在
，
的被调查者中各随机选取两人进行追踪调查，记选中的4人中不赞成“车辆限行”的人数为
，求随机变量的分布列和数学期望. 
已知中心在原点，焦点在x轴上的椭圆C的离心率为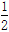 
，且经过点M
．
（1）求椭圆C的方程；
（2）是否存在过点P（2，1）的直线l1与椭圆C相交于不同的两点A，B，满足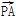
·
＝
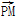2？若存在，求出直线l1的方程；若不存在，请说明理由．
从含有两件正品a1，a2和一件次品b1的3件产品中每次任取1件，
每次取出后不放回，连续取两次．
（1）求取出的两件产品中恰有一件次品的概率；
（2）如果将“每次取出后不放回”这一条件换成“每次取出后放回”，则取出的两件产品中恰有一件次品的概率是多少？
设命题p：实数x满足x2－4ax＋3a2<0，其中a>0，命题q：实数x满足
（1）若a＝1，且p∧q为真，求实数x的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．
一个袋中有红、白两种球各若干个，现从中一次性摸出两个球，假设摸出的两个球至少有一个红球的概率为
，至少一个白球的概率为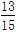
，求摸出的两个球恰好红球白球各一个的概率．
已知抛物线
上点
到焦点
的距离为4．
（1）求
，
值；
（2）设
，
是抛物线上分别位于
轴两侧的两个动点，且
（其中
为坐标原点）．求证：直线
过定点，并求出该定点的坐标．