某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数 的方差是多少?
的方差是多少?
如图,四棱锥P—ABCD中,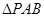 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,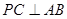 ,E为PD点上一点,满足
,E为PD点上一点,满足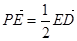
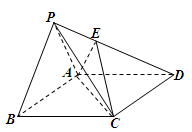
(1)证明:平面ACE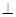 平面ABCD;
平面ABCD;
(2)求直线PD与平面ACE所成角正弦值的大小.
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课程 |
初等代数 |
初等几何 |
初等数论 |
微积分初步 |
| 合格的概率 |
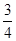 |
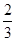 |
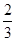 |
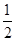 |
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记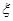 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求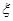 的分布列及期望
的分布列及期望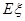 .
.
已知函数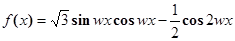 ,
,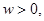
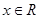 且函数
且函数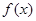 的最小正周期为
的最小正周期为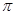 .
.
(1)求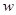 的值和函数
的值和函数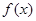 的单调增区间;
的单调增区间;
(2)在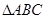 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是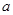 、
、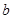 、
、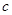 ,又
,又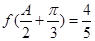 ,
,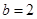 ,
,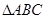 的面积等于
的面积等于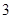 ,求边长
,求边长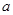 的值.
的值.
数列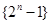 的前
的前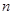 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取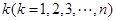 个数,其所有可能的
个数,其所有可能的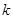 个数的乘积的和为
个数的乘积的和为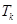 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,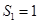 ;当
;当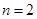 时,
时, ,
, ,
,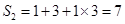 .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想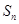 ,并用数学归纳法证明.
,并用数学归纳法证明.
如图(1),等腰直角三角形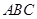 的底边
的底边 ,点
,点 在线段
在线段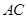 上,
上,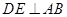 于
于 ,现将
,现将 沿
沿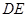 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
(Ⅰ)求证: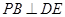 ;
;
(Ⅱ)若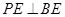 ,直线
,直线 与平面
与平面 所成的角为
所成的角为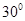 ,求
,求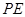 长.
长.