如图,点C在以AB为直径的半圆O上,以点A为旋转中心,以∠β(0°<β<90°)为旋转角度将B旋转到点D,过点D作DE⊥AB于点E,交AC于点F,过点C作圆O的切线交DE于点G。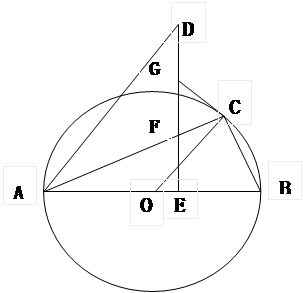
(1)求证:∠GCA=∠OCB;
(2)设∠ABC=m°,求∠DFC的值;
(3)当G为DF的中点时,请探究∠β与∠ABC的关系,并说明理由。
如图,已知锐角△ABC.
(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,若BC=5,AD=4,tan∠BAD=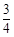 ,求DC的长.
,求DC的长.
某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
(1)参加这次跳绳测试的共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对应的圆心角的度数是 ;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.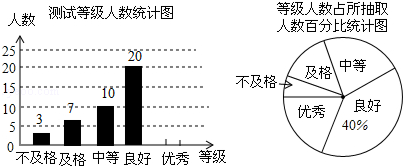
某校体育社团在校内开展“最喜欢的体育项目(四项选一项)”调查,对九年级学生随机抽样,并将收集的数据绘制成如图两幅不完整的统计图,请结合统计图解答下列问题: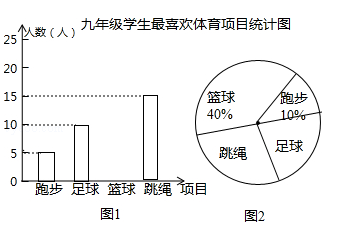
(1)求本次抽样人数有多少人?
(2)补全条形统计图;
(3)该校九年级共有600名学生,估计九年级最喜欢跳绳项目的学生有多少人?
在一个不透明的袋中装有2个黄球,3个黑球和5个红球,它们除颜色外其他都相同.
(1)将袋中的球摇均匀后,求从袋中随机摸出一个球是黄球的概率;
(2)现在再将若干个红球放入袋中,与原来的10个球均匀混合在一起,使从袋中随机摸出一个球是红球的概率是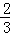 ,请求出后来放入袋中的红球的个数.
,请求出后来放入袋中的红球的个数.
某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图: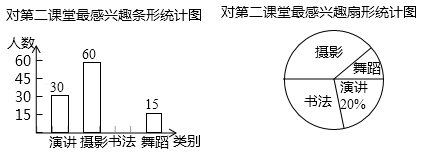
(1)此次调查抽取的学生人数m= 名,其中选择“书法”的学生占抽样人数的百分比n= ;
(2)若该校有3000名学生,请根据以上数据估计该校对“书法”最感兴趣的学生人数.