称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列” 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
在编号1~9的九个盒子中,共 放有351粒
放有351粒 米,己知每个盒子都比前一号盒子多放同样粒数的米
米,己知每个盒子都比前一号盒子多放同样粒数的米 。
。
(1)如果1 号盒子内放了11粒米,那么后面的盒子比它前一号的盒子多放几粒米?
号盒子内放了11粒米,那么后面的盒子比它前一号的盒子多放几粒米?
(2)如果3号盒子内放了23粒米,那么后面的盒子比它前一号的盒子多放几粒米?
已知向量
⑴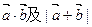 ;
;
⑵若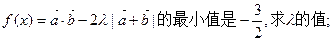
已知向量a ,向量b
,向量b ,若
,若 a ·b +1 .
a ·b +1 .
(I)求函数 的解析式和最小正周期;
的解析式和最小正周期;
(II) 若 ,求
,求 的最大值和最小值.
的最大值和最小值.
已知向量
(1)当 时,求
时,求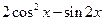 的值;
的值;
(2) 求
求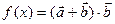 在
在 上的值域.
上的值域.
(本题12分)
已知M= (1+cos2x,1),N=(1,
(1+cos2x,1),N=(1, sin2x+a)(x,a∈R,a是常数),且y=
sin2x+a)(x,a∈R,a是常数),且y= ·
· (O是坐标原点)
(O是坐标原点)
⑴求y关于x的函数关系式y=f(x);
⑵若x∈[0, ],f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由y=2sin(x+
],f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由y=2sin(x+ )
) 的图象经过怎样的变换而得到
的图象经过怎样的变换而得到