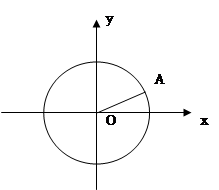
如图,设 是单位圆上一点,一个动点从点
是单位圆上一点,一个动点从点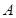 出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周.
出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周.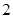 秒时,动点到达点
秒时,动点到达点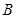 ,
,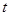 秒时动点到达点
秒时动点到达点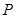 .设
.设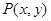 ,其纵坐标满足
,其纵坐标满足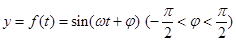 .
.
(1)求点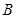 的坐标,并求
的坐标,并求 ;
;
(2)若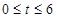 ,求
,求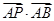 的取值范围.
的取值范围.
设 为关于n的k
为关于n的k 次多项式.数列{an}的首项
次多项式.数列{an}的首项 ,前n项和为
,前n项和为 .对于任意的正整数n,
.对于任意的正整数n, 都成立.
都成立.
(1)若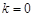 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列
若函数 为定义域
为定义域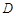 上单调函数,且存在区间
上单调函数,且存在区间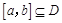 (其中
(其中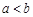 ),使得当
),使得当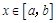 时,
时, 的取值范围恰为
的取值范围恰为 ,则称函数
,则称函数 是
是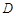 上的正函数,区间
上的正函数,区间 叫做等域区间.
叫做等域区间.
(1)已知 是
是 上的正函数,求
上的正函数,求 的等域区间;
的等域区间;
(2)试探究是否存在实数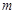 ,使得函数
,使得函数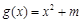 是
是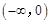 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数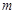 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
若椭圆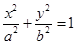 (
(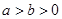 )过点
)过点 ,离心率为
,离心率为 ,
,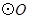 的圆心为原点,直径为椭圆的短轴,
的圆心为原点,直径为椭圆的短轴,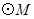 的方程为
的方程为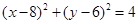 ,过
,过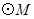 上任一点
上任一点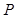 作
作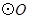 的切线
的切线 ,
,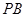 ,切点为
,切点为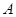 ,
, 。
。
(1)求椭圆的方程;
(2)若直线 与
与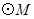 的另一交点为
的另一交点为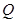 ,当弦
,当弦 最大时,求直线
最大时,求直线 的方程;
的方程;
(3)求 的最大值与最小值。
的最大值与最小值。
如图,某兴趣小组测得菱形养殖区 的固定投食点
的固定投食点 到两条平行河岸线
到两条平行河岸线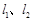 的距离分别为4m、8m,河岸线
的距离分别为4m、8m,河岸线 与该养殖区的最近点
与该养殖区的最近点 的距离为1m,
的距离为1m,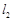 与该养殖区的最近点
与该养殖区的最近点 的距离为2m.
的距离为2m.
(1)如图甲,养殖区在投食点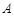 的右侧,若该小组测得
的右侧,若该小组测得 ,请据此算出养殖区的面积;
,请据此算出养殖区的面积;
(2)如图乙,养殖区在投食点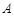 的两侧,试在该小组未测得
的两侧,试在该小组未测得 的大小的情况下,估算出养殖区的最小面积.
的大小的情况下,估算出养殖区的最小面积.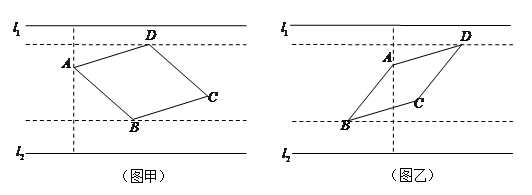
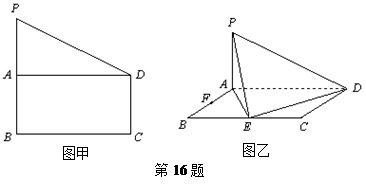
如图甲,在直角梯形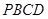 中,
中, ,
, ,
,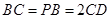 ,
,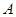 是
是 的中点. 现沿
的中点. 现沿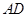 把平面
把平面 折起,使得
折起,使得 (如图乙所示),
(如图乙所示),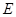 、
、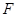 分别为
分别为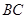 、
、 边的中点.
边的中点.
(Ⅰ)求证: 平面
平面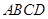 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)在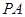 上找一点
上找一点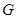 ,使得
,使得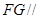 平面
平面 .
.