已知函数 ,
,
(1)在如图给定的直角坐标系内画出 的图象;
的图象;
(2)写出 的单调递增区间.
的单调递增区间.
(本小题满分14分)
已知向量 ,其中
,其中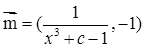 ,
,
 ,把其中
,把其中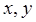 所满足的关系式记为
所满足的关系式记为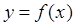 ,且函数
,且函数 为奇函数.
为奇函数.
(1)求函数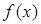 的表达式;
的表达式;
(2)已知数列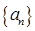 的各项都是正数,
的各项都是正数, 为数列
为数列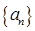 的前
的前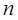 项和,且对于任意
项和,且对于任意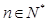 ,都有“数列
,都有“数列 的前
的前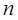 项和”等于
项和”等于 ,求数列
,求数列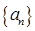 的首项
的首项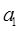 和通项公式
和通项公式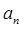 ;
;
(3)若数列 满足
满足 ,求数列
,求数列 的最小值.
的最小值.
(本小题满分14分)已知圆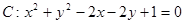 ,直线
,直线 ,直线
,直线 与圆
与圆 交于
交于 两点,点
两点,点 的坐标为
的坐标为 ,且满足
,且满足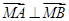 .
.
(1)当 时,求
时,求 的值;
的值;
(2)当 时,求
时,求 的取值范围.
的取值范围.
(本小题满分14分)某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
| 资金 |
单位产品所需资金(百元) |
月资金供应量(百元) |
|
| 空调机 |
洗衣机 |
||
| 成本 |
30 |
20 |
300 |
| 劳动力(工资) |
5 |
10 |
110 |
| 单位利润 |
6 |
8 |
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
(本小题满分14分)四棱锥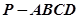 中,底面
中,底面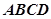 是正方形,
是正方形,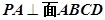 ,垂足为点
,垂足为点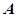 ,
,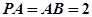 ,点
,点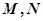 分别是
分别是 的中点.
的中点.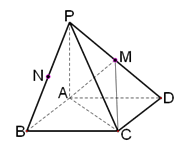
(1)求证: ;
;
(2)求证: ;
;
(3)求四面体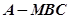 的体积.
的体积.
在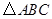 中,
中,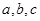 分别为角
分别为角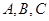 所对的边长,已知
所对的边长,已知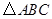 的周长为
的周长为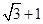 ,
,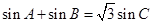 ,且
,且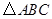 的面积为
的面积为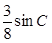 .
.
(1)求边 的长;
的长;
(2)求 的值.
的值.