设二次函数 满足下列条件:①当
满足下列条件:①当 时,
时, 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线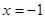 对称;②当
对称;②当 时,
时,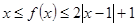 恒成立.
恒成立.
(1)求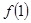 的值;
的值;
(2)求 的解析式;
的解析式;
(3)若 在区间
在区间 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数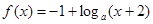 (a>0,且a≠1),
(a>0,且a≠1),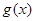 =
=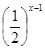 .
.
(1)函数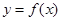 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;
(2)若函数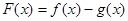 的图像过点(2,
的图像过点(2,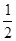 ),证明:函数
),证明:函数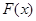 在
在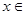 (1,2)上有唯一的零点.
(1,2)上有唯一的零点.
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1的一条折线表示;西红柿的种植成本与上市时间的关系用图2的抛物线表示.
(1)写出图1表示的市场售价与时间的函数关系式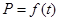 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式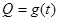 .
.
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/百千克,时间单位:天)
已知函数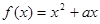 ,且对任意的实数
,且对任意的实数 都有
都有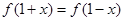 成立.
成立.
(1)求实数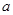 的值;
的值;
(2)利用函数单调性的定义证明函数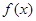 在区间
在区间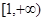 上是增函数.
上是增函数.
已知函数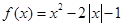 .
.
(1)证明函数 是偶函数;
是偶函数;
(2)在如图所示的平面直角坐标系中作出函数 的图象.
的图象.