如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,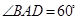 ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.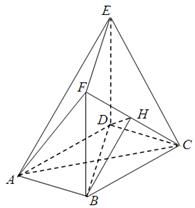
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求直线DH与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的大小.
的大小.
某高级中学共有学生3000名,各年段男、女学生人数如下表
| 高一年 |
高二年 |
高三年 |
|
| 女生 |
523 |
x |
Y |
| 男生 |
487 |
490 |
z |
已知在全校学生中随机抽取1名,抽到高二女生的概率为0.17,
(1)问高二年段女生有多少名?
现对各年段采用分层抽样的方法,在全校抽取300名学生,问应在高三年段抽取多少名学生
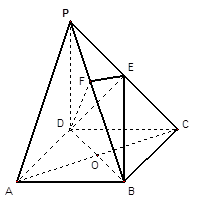
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求 .
.
如图,正四棱锥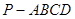 中,侧棱
中,侧棱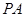 与底面
与底面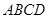 所成角的正切值为
所成角的正切值为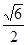 .
.
(1)求侧面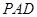 与底面
与底面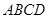 所成二面角的大小;
所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.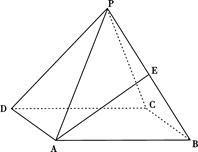
已知 中
中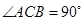 ,
,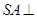 面
面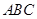 ,
, ,求证:
,求证: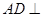 面
面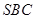 .
.
某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.规定:每辆自行车的日租金不超过20元,每辆自行车的日租金 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用
元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用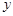 表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得).
表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得).
(1)求函数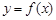 的解析式及定义域;
的解析式及定义域;
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?