已知集合 ,对于数列
,对于数列 中
中 .
.
(Ⅰ)若三项数列 满足
满足 ,则这样的数列
,则这样的数列 有多少个?
有多少个?
(Ⅱ)若各项非零数列 和新数列
和新数列 满足首项
满足首项 ,
, (
( ),且末项
),且末项 ,记数列
,记数列 的前
的前 项和为
项和为 ,求
,求 的最大值.
的最大值.
(本小题满分12分)已知函数 (
( 为常数,
为常数, 为自然对数的底数)是实数集
为自然对数的底数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数.
(1)求实数 的值;
的值;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数.
的根的个数.
(本小题满分12分)已知等比数列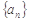 是递增数列,
是递增数列,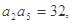
 ,又数列
,又数列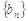 满足
满足 ,
,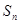 是数列
是数列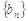 的前
的前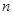 项和.
项和.
(1)求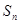 ;
;
(2)若对任意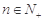 ,都有
,都有 成立,求正整数
成立,求正整数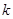 的值
的值
(本小题满分12分)在三角形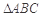 中,
中,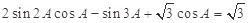
(1)求角A的大小;
(2)已知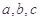 分别是内角
分别是内角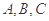 的对边,若
的对边,若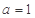 且
且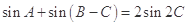 ,求三角形
,求三角形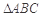 的面积.
的面积.
(本小题满分12分)已知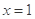 是
是 的一个极值点.
的一个极值点.
(1)求函数 的单调减区间;
的单调减区间;
(2)设函数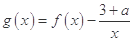 ,若函数
,若函数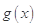 在区间
在区间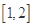 内单调递增,求
内单调递增,求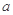 的取值范围.
的取值范围.
(本小题满分12分)已知 ,
,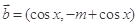 , 且
, 且 .
.
(1)求函数 的解析式;并求其最小正周期和对称中心;
的解析式;并求其最小正周期和对称中心;
(2)当 时,
时,  的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 并求出相应的
的最大值, 并求出相应的 的值.
的值.