如图,在四棱锥 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,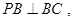
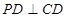 ,且
,且 点满足
点满足 .
. 
(1)证明: 平面
平面 .
.
(2)在线段 上是否存在点
上是否存在点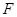 ,使得
,使得 平面
平面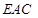 ?若存在,确定点
?若存在,确定点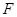 的位置,若不存在请说明理由 .
的位置,若不存在请说明理由 .
有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问: 工人师傅是怎样选择矩形的四点的?并求出最大面积值.
用一块长为a,宽为b(a>b)的矩形木板,在二面角为α的墙角处围出一个直三棱柱的谷仓,试问应怎样围才能使谷仓的容积最大?并求出谷仓容积的最大值.
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。
(1)求证: b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值.
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求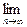 xn
xn
据有关资料,1995年我国工业废弃垃圾达到7.4×108吨,占地562.4平方公里,若环保部门每年回收或处理1吨旧物资,则相当于处理和减少4吨工业废弃垃圾,并可节约开采各种矿石20吨,设环保部门1996年回收10万吨废旧物资,计划以后每年递增20%的回收量,试问:
(1)2001年回收废旧物资多少吨?
(2)从1996年至2001年可节约开采矿石多少吨(精确到万吨)?
(3)从1996年至2001年可节约多少平方公里土地?