据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:

|
应该取消 |
应该保留 |
无所谓 |
||
| 在校学生 |
2100人 |
120人 |
y人 |
||
| 社会人士 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
(本小题满分14分)
已知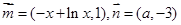
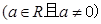 , 函数
, 函数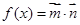 .
.
(Ⅰ)求函数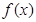 的单调区间;
的单调区间;
(Ⅱ)若函数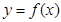 的图像在点
的图像在点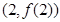 处的切线的斜率为
处的切线的斜率为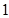 ,问:
,问: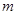 在什么范围
在什么范围
取值时,对于任意的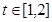 ,函数
,函数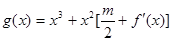 在区间
在区间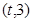 上总存在
上总存在
极值?
(Ⅲ)当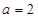 时,设函数
时,设函数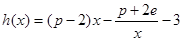 ,若在区间
,若在区间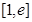 上至少存在
上至少存在
一个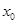 ,使得
,使得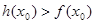 成立,试求实数
成立,试求实数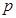 的取值范围.
的取值范围.
(本小题满分12分)
给定椭圆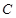 :
: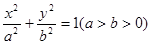 ,称圆心在原点
,称圆心在原点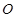 ,半径为
,半径为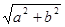 的圆是
的圆是
椭圆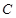 的“准圆”。若椭圆
的“准圆”。若椭圆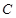 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到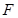 的距
的距
离为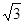 .
.
(Ⅰ)求椭圆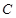 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点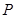 是椭圆
是椭圆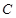 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点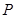 作直线
作直线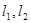 使得
使得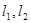 与椭
与椭
圆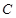 都只有一个交点,且
都只有一个交点,且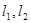 分别交其“准圆”于点
分别交其“准圆”于点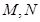 ;
;
(1)当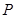 为“准圆”与
为“准圆”与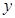 轴正半轴的交点时,求
轴正半轴的交点时,求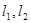 的方程.
的方程.
(2)求证: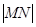 为定值.
为定值.
(本小题满分12分)
已知单调递增的等比数列{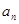 }满足:
}满足: ,且
,且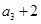 是
是 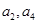 的等差中
的等差中
项.(1)求数列{an}的通项公式.
(2)若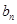 =
=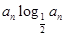 ,sn为数列
,sn为数列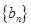 的前
的前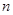 项和,求证:sn
项和,求证:sn
 .
.
(本小题满分12分)
如图,已知矩形 所在平面与矩形
所在平面与矩形 所在平面垂直,
所在平面垂直, ,
,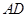 =1,
=1,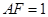 ,
,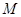 是线段
是线段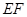 的中点.
的中点.
(1)求证: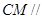 平面
平面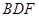 ;
;
(2)求二面角 的正弦值;
的正弦值;
(3)求多面体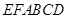 的体积.
的体积.
(本小题满分12分)
某校为宣传县教育局提出的“教育发展,我的责任”教育实践活动,要举行一次以“我
为教育发展做什么”为主题的的演讲比赛,比赛分为初赛、复赛、决赛三个阶段进行,已知
某选手通过初赛、复赛、决赛的概率分别是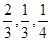 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在比赛中比赛的次数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.