（本小题满分12分）
某校为宣传县教育局提出的“教育发展，我的责任”教育实践活动，要举行一次以“我
为教育发展做什么”为主题的的演讲比赛，比赛分为初赛、复赛、决赛三个阶段进行，已知
某选手通过初赛、复赛、决赛的概率分别是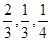
，且各阶段通过与否相互独立.
（I）求该选手在复赛阶段被淘汰的概率；
（II）设该选手在比赛中比赛的次数为
，求的分布列、数学期望和方差.
设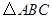
的内角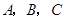
所对的边长分别为
，且
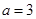，A=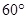
，
．
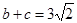（1）求函数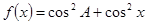
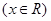的单调递增区间及最大值；
（2）求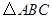的面积的大小
已知函数
，
（
）
（1）对于函数
中的任意实数x，在
上总存在实数
，使得
成立，求实数
的取值范围
（2）设函数
，当
在区间
内变化时，
（1）求函数
的取值范围；
（2）若函数
有零点，求实数m的最大值.
设椭圆C1：
的右焦点为F，P为椭圆上的一个动点．
（1）求线段PF的中点M的轨迹C2的方程；
（2）过点F的直线l与椭圆C1相交于点A、D，与曲线C2顺次相交于点B、C，当
时，求直线l的方程．
如图，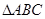
在平面
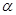内，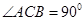
，AB=2BC=2，P为平面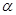外一个动点，且PC=
，
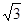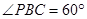
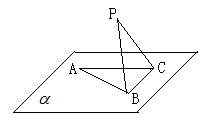
（1）问当PA的长为多少时，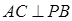
（2）当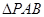
的面积取得最大值时，求直线PC与平面PAB所成角的正弦值
在数列{an}中，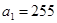
，
，
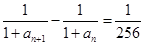
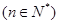（1）求数列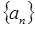
的通项公式
（2）设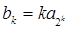
（
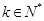），记数列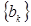
的前k项和为
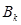，求
的最大值．