(本小题满分14分)
已知函数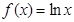 的图象是曲线C,点
的图象是曲线C,点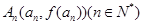 是曲线C上的一系列点,
是曲线C上的一系列点,
曲线C在点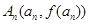 处的切线与y轴交于点
处的切线与y轴交于点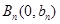 。若数列
。若数列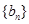 是公差为2的等差
是公差为2的等差
数列,且
(1)分别求出数列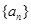 与数列
与数列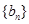 的通项公式;
的通项公式;
(2)设O为坐标原点, 表示
表示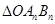 的面积,求数列
的面积,求数列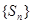 的前项n和
的前项n和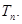
(本小题满分14分)
如图,设P是圆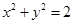 上的动点,点D是P在x轴上的投影。M为线段PD上一点,
上的动点,点D是P在x轴上的投影。M为线段PD上一点,
且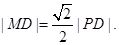
(1)当点P在圆上运动时,求点M的轨迹C的方程;
(2)已知点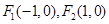 ,设点
,设点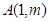
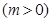 是轨迹C上的一点,求
是轨迹C上的一点,求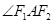 的
的
平分线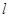 所在直线的方程。
所在直线的方程。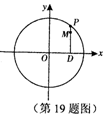
(本小题满分14分)
如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1。
将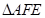 沿折起到
沿折起到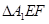 的位置,使平面
的位置,使平面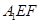 与平面BCFE垂直,连结A1B、A1P(如图2)。
与平面BCFE垂直,连结A1B、A1P(如图2)。
(1)求证:PF//平面A1EB;
(2)求证:平面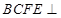 平面A1EB;
平面A1EB;
(3)求四棱锥A1—BPFE的体积。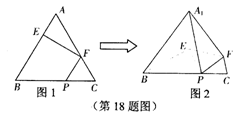
(本小题满分12分)
某校一个甲类班x名学生在2011年某次数学测试中,成绩全部介于90分与140分之间,
将测试结果按如下方式分成五组,第一组 ;第二组
;第二组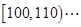 第五组
第五组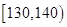 ,
,
下表是按上述分组方法得到的频率分布表: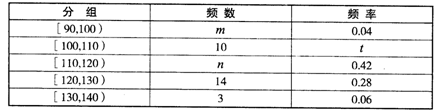
(1)求x及分布表中m,n,t的值;
(2)设a,b是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件“ 的概率。”
的概率。”
.(本小题满分12分)
已知向量 ,且
,且
(1)求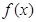 的解析式和它的最小正周期;
的解析式和它的最小正周期;
(2)求函数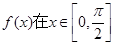 的值域。
的值域。