已知圆心为点 的圆与直线
的圆与直线 相切.
相切.
(1)求圆 的标准方程;
的标准方程;
(2)对于圆 上的任一点
上的任一点 ,是否存在定点
,是否存在定点 (不同于原点
(不同于原点 )使得
)使得 恒为常数?若存在,求出点
恒为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
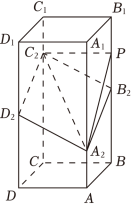
如图,在正四棱柱 中, , .点 , , , 分别在棱 , , , 上, , , .
(1)证明: ;
(2)点 在棱 上,当二面角 为 时,求 .
已知在 中, , .
(1)求 ;
(2)设 ,求 边上的高.
[选修4-5:不等式选讲]
已知 .
(1)求不等式 的解集;
(2)在直角坐标系 中,求不等式组 所确定的平面区域的面积.
[选修4-4:坐标系与参数方程]
在直角坐标系 中,以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 ,曲线 ( 为参数, ).
(1)写出 的直角坐标方程;
(2)若直线 既与 没有公共点,也与 没有公共点、求 的取值范围.
已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)是否存在 , ,使得曲线 关于直线 对称,若存在,求 , 的值,若不存在,说明理由;
(3)若 在 存在极值,求 的取值范围.