学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数
与听课时间
（单位：分钟）之间的关系满足如图所示的图像，当
时，图像是二次函数图像的一部分，其中顶点
，过点
；当
时，图像是线段
，其中
，根据专家研究，当注意力指数大于62时，学习效果最佳.
（1）试求
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由.
(本小题满分10分)
已知函数f (x)=a+bsinx+2cosx(x∈R)的图象经过点A(0,1),B
.
(1)求函数f (x)的单调递减区间；
(2)由函数y=f (x)的图象经过平移是否能得到一个奇函数y=g(x)的图象？若能，请写出平移过程；若不能，请说明理由.
甲乙两位同学参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
（1）用茎叶图表示这两组数据；
（2）现要从中选派一人参加数学竞赛，从统计学的角度考虑，你认为选派哪位学生参加合适？请说明理由；
（3）若将频率视为概率，对甲同学在今后的3次数学竞赛成绩进行预测，记这3次成绩中高于80分的次数为X，求X的分布列及数学期望
。
甲、乙两人各射击一次，击中目标的概率分别是
和
。假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响。
（Ⅰ）求甲射击4次，至少1次未击中目标的概率；
（Ⅱ）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（Ⅲ）假设连续两次未击中目标，则停止射击。问：乙恰好射击5次后，被中止射击的概率是多少？
某高级中学共有3000名学生，各年级男、女生人数如下表：
| 高一 |
高二 |
高三 |
|
| 女生 |
523 |
x |
y |
| 男生 |
487 |
490 |
z |
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0．17．
（1）问高二年级有多少名女生？
（2）现对各年级用分层抽样的方法在全校抽取300名学生，问应在高三年级抽取多少名学生？
已知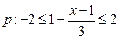
，
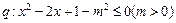，且
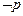是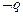
的必要不充分条件，求实数
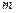的取值范围．