已知椭圆 :
: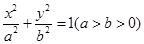 经过点
经过点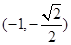 ,
,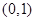 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左、右焦点分别为
的左、右焦点分别为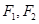 ,过点
,过点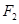 的直线交椭圆
的直线交椭圆 于
于 两点,求
两点,求 面积的最大值.
面积的最大值.
已知等差数列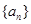 的前
的前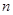 项和为
项和为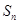 ,并且
,并且 ,
,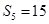 ,数列
,数列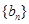 满足:
满足: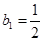 ,
,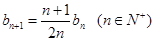 ,记数列
,记数列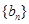 的前
的前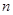 项和为
项和为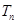 .
.
(1)求数列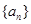 的通项公式
的通项公式 及前
及前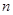 项和公式
项和公式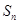 ;
;
(2)求数列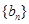 的通项公式
的通项公式 及前
及前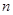 项和公式
项和公式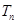 ;
;
(3)记集合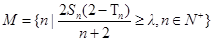 ,若
,若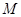 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围。
的取值范围。
如图,已知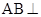 平面
平面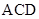 ,
,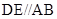 ,△
,△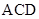 是正三角形,
是正三角形, ,且
,且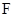 是
是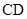 的中点.
的中点.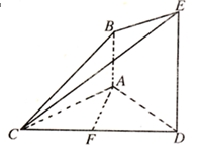
(1)求证: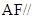 平面
平面 ;
;
(2)求证:平面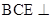 平面
平面 ;
;
(3)求平面 与平面
与平面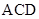 所成锐二面角的大小.
所成锐二面角的大小.
在株洲市二中组织的“青春杯”篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮.现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是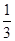 ,
,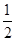 .两人共投篮3次,且第一次由甲开始投篮.假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮.假设每人每次投篮命中与否均互不影响.
(1)求3次投篮的人依次是甲、甲、乙的概率;
(2)若投篮命中一次得1分,否则得0分.用ξ表示甲的总得分,求ξ的分布列和数学期望.
在△ABC中,已知A=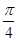 ,
, .
.
(1)求cosC的值;
(2)若BC=2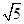 ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长.
(本小题满分14分)已知函数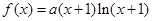 图像上的点
图像上的点 处的切线与直线
处的切线与直线 垂直
垂直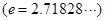 .
.
(1)求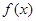 的单调区间;
的单调区间;
(2)求函数 与
与
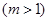 的图象在区间
的图象在区间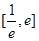 上交点的个数;
上交点的个数;
(3)证明:当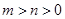 时,
时, .
.