数列 的前
的前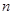 项和为
项和为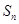 ,且
,且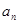 是
是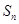 和
和 的等差中项,等差数列
的等差中项,等差数列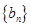 满足
满足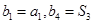
(1)求数列 、
、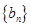 的通项公式
的通项公式
(2)设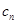 =
=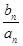 ,求数列
,求数列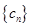 的前
的前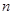 项和
项和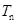 .
.
(本小题满分12分)双曲线与椭圆 有相同焦点,且经过点
有相同焦点,且经过点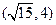 .
.
(1)求双曲线的方程;
(2)求双曲线的离心率.
(本小题满分12分)为了检测某种产品的质量,抽取了一个容量为40的样本,检
测结果为一等品8件,二等品18件,三等品12件,次品2件.
(1)列出样本的频率分布表;
(2)画出表示样本频率分布的条形图;
(3)根据上述结果,估计此种新产品为二等品或三等品的概率是多少?
已知二次函数 的图象过点(1,13),且函数
的图象过点(1,13),且函数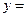
 是偶函数.
是偶函数.
(1)求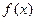 的解析式;
的解析式;
(2)已知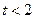 ,
,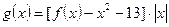 ,求函数
,求函数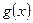 在[
在[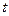 ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(3)函数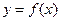 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
已知a>0且a≠1, 。
。
(1)判断函数f(x)是否有零点,若有求出零点;
(2)判断函数f(x)的奇偶性;
(3)讨论f(x)的单调性并用单调性定义证明。