如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面 底面
底面 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
(1)求证:EF//平面PAD;
(2)求证:平面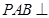 平面
平面 .
.
已知数列 的前n项和为Sn,且
的前n项和为Sn,且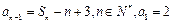 .
.
(1)求数列 的通项;
的通项;
(2)设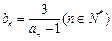 ,求
,求 .
.
在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
已知数列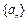 的前
的前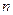 项和为
项和为 ,点
,点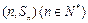 均在函数
均在函数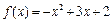 的图象上
的图象上
(1)求数列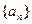 的通项公式
的通项公式
(2)若数列 的首项是1,公比为
的首项是1,公比为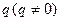 的等比数列,求数列
的等比数列,求数列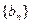 的前
的前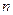 项和
项和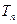 .
.
函数 是
是 的导函数.
的导函数.
(Ⅰ)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)若 的值.
的值.
(本小题满分14分)给定函数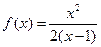
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,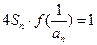 求证:
求证: ;
;
(3)设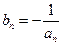 ,
,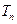 为数列
为数列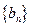 的前
的前 项和,求证:
项和,求证: 。
。