某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如图所示.
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
 |
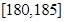10 |
0.100 |
| 合计 |
100 |
1.00 |
（1）请先求出频率分布表中①、②位置相应的数据，再在答题卷上完成下列频率分布直方图；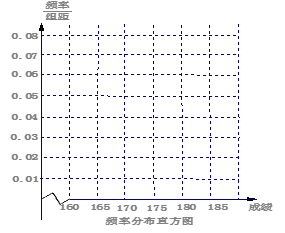
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官进行面试，求：第4组至少有一名学生被考官A面试的概率？
已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点B恰好是抛物线
的焦点，且离心率等于
，直线
与椭圆C交于M，N两点。
（1）求椭圆C的方程；
（2）椭圆C的右焦点F是否可以为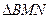
的垂心？若可以，求出直线的方程；若不可以，请说明理由。
已知平行四边形
的顶点
，
，
求顶点
的坐标．
一条河的两岸平行，河的宽度
m，一艘船从
处出发到河对岸．已知船的速度
km/h，水流速度
km/h．要使船行驶的时间最短，那么船行驶的距离与合速度的比值必须最小．此时我们分三种情况讨论：
（１）当船逆流行驶，与水流成钝角时；
（２）当船顺流行驶，与水流成锐角时；
（３）当船垂直于对岸行驶，与水流成直角时．
请同学们计算上面三种情况，是否当船垂直于对岸行驶时，与水流成直角时，所用时间最短
设
，
是平面内一组基底，证明：当
时，恒有
．
如图，已知
，
，任意点
关于点
的对称点为
，点关于点
的对称点为
，用
、
表示向量
．
