如图,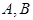 是椭圆
是椭圆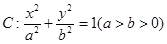 的左、右顶点,椭圆
的左、右顶点,椭圆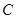 的离心率为
的离心率为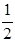 ,右准线
,右准线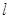 的方程为
的方程为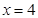 .
.
(1)求椭圆方程;
(2)设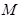 是椭圆
是椭圆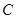 上异于
上异于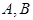 的一点,直线
的一点,直线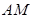 交
交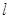 于点
于点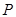 ,以
,以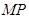 为直径的圆记为
为直径的圆记为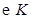 . ①若
. ①若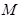 恰好是椭圆
恰好是椭圆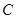 的上顶点,求
的上顶点,求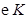 截直线
截直线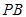 所得的弦长;
所得的弦长;
②设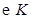 与直线
与直线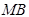 交于点
交于点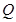 ,试证明:直线
,试证明:直线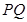 与
与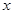 轴的交点
轴的交点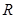 为定点,并求该定点的坐标.
为定点,并求该定点的坐标.
已知等差数列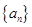 的首项
的首项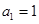 ,公差
,公差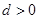 ,且
,且 、
、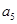 、
、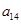 分别是等比数列
分别是等比数列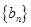 的
的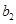 、
、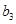 、
、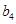 .
.
(1)求数列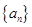 和
和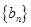 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数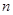 均有
均有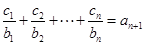 成立,求
成立,求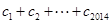 的值.
的值.
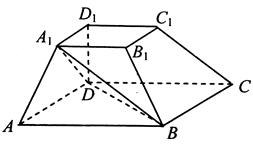
如图,在四棱台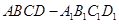 中,底面
中,底面 是平行四边形,
是平行四边形,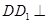 平面
平面 ,
,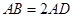 ,
, ,
, .
.
(1)证明: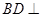 平面
平面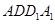 ;
;
(2)证明: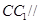 平面
平面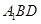 .
.
某工厂有工人 人,其中
人,其中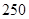 名工人参加过短期培训(称为
名工人参加过短期培训(称为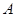 类工人),另外
类工人),另外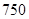 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按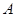 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1)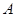 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从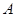 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 |
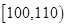 |
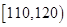 |
 |
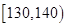 |
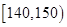 |
| 人数 |
 |
 |
 |
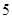 |
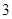 |
表2
| 生产能力分组 |
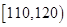 |
 |
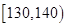 |
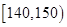 |
| 人数 |
 |
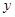 |
 |
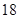 |


①求 、
、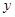 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;
②分别估计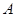 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
中的数据用该组区间的中点值作代表).
设函数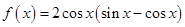 .
.
(1)求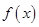 的最小正周期;
的最小正周期;
(2)求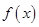 的单调递减区间.
的单调递减区间.
已知函数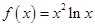 .
.
(1)求函数 的单调区间;
的单调区间;
(2)证明:对任意的 ,存在唯一的
,存在唯一的 ,使
,使 ;
;
(3)设(2)中所确定的 关于
关于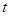 的函数为
的函数为 ,证明:当
,证明:当 时,有
时,有 .
.