已知数列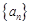 的前
的前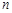 项和
项和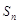 满足
满足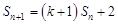 ,又
,又 ,
,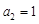 .
.
(1)求实数k的值;
(2)问数列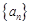 是等比数列吗?若是,给出证明;若不是,说明理由;
是等比数列吗?若是,给出证明;若不是,说明理由;
(3)求出数列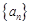 的前
的前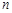 项和
项和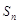 .
.
椭圆 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点
(1)求椭圆 的标准方程和动点
的标准方程和动点 的轨迹
的轨迹 的方程。
的方程。
(2)过椭圆 的右焦点
的右焦点 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求 的面积。
的面积。
(3)设轨迹 与
与 轴交于点
轴交于点 ,不同的两点
,不同的两点 在轨迹
在轨迹 上,
上,
满足 求证:直线
求证:直线 恒过
恒过 轴上的定点。
轴上的定点。
如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2。
|
(1)证明:AB1⊥BC1;
(2)求点B到平面AB1C1的距离;本题10分)如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
(1)一条船船顶部宽4m,要使这艘船安全通过,则船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
已知圆C经过A(1, ),B(5,3),并且圆的面积被直线
),B(5,3),并且圆的面积被直线 :
: 平分.求圆C的方程;
平分.求圆C的方程;
已知命题P:方程 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围