设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点,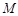 为线段
为线段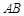 的中点.
的中点.
(1)问:直线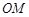 与
与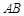 能否垂直?若能,求
能否垂直?若能,求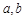 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知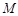 为
为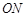 的中点,且
的中点,且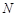 点在椭圆上.若
点在椭圆上.若 ,求
,求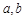 之间满足的关系式.
之间满足的关系式.
(本题满分14分)四棱锥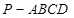 的底面
的底面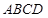 是直角梯形,
是直角梯形,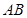 ∥
∥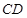 ,
,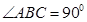 ,
, ,
,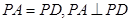 ,
,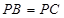
(Ⅰ)求证:平面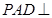 平面
平面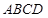 ;
;
(Ⅱ)求直线 与平面
与平面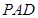 所成角的正切值.
所成角的正切值.
(本题满分14分)设等比数列 的首项为
的首项为 ,公比
,公比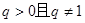 ,前
,前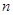 项和为
项和为
(Ⅰ)当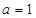 时,
时, 三数成等差数列,求数列
三数成等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数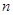 ,命题甲:
,命题甲: 三数构成等差数列.
三数构成等差数列.
命题乙: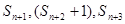 三数构成等差数列.
三数构成等差数列.
求证:对于同一个正整数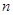 ,命题甲与命题乙不能同时为真命题.
,命题甲与命题乙不能同时为真命题.
(本题满分14分)设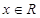 ,向量
,向量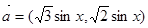 ,
,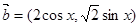 ,函数
,函数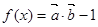 .(Ⅰ)在区间
.(Ⅰ)在区间 内,求
内,求 的单调递减区间;
的单调递减区间;
(Ⅱ)若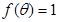 ,其中
,其中 ,求
,求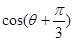 .
.
设 x1、x2(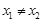 )是函数
)是函数  (
( )的两个极值点.(I)若
)的两个极值点.(I)若 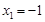 ,
,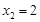 ,求函数
,求函数  的解析式;
的解析式;
(II)若 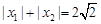 ,求 b 的最大值;
,求 b 的最大值;
(III)设函数 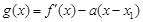 ,
,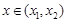 ,当
,当 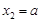 时,求
时,求 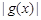 的最大值.
的最大值.
设椭圆 C1: (
( )的一个顶点与抛物线 C2:
)的一个顶点与抛物线 C2: 的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率
的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点 F2 的直线
,过椭圆右焦点 F2 的直线  与椭圆 C 交于 M,N 两点.
与椭圆 C 交于 M,N 两点.
(I)求椭圆C的方程;
(II)是否存在直线  ,使得
,使得  ,若存在,求出直线
,若存在,求出直线  的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(III)若 AB 是椭圆 C 经过原点 O 的弦,MN//AB,求证: 为定值.
为定值.