已知函数 ,xÎR.
,xÎR.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数
单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.
已知集合M={x|2x-4=0},集合N={x|x2-3x+m=0},
(1)当m=2时,求M∩N,M∪N;
(2)当M∩N=Ø时,求实数m的取值范围.
已知函数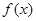

(1)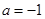 时,求函数
时,求函数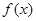 定义域;
定义域;
(2)当 时,函数
时,函数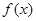 有意义,求实数
有意义,求实数 的取值范围;
的取值范围;
(3)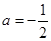 时,函数
时,函数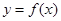 的图像与
的图像与
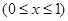 无交点,求实数
无交点,求实数 的取值范围.
的取值范围.
设 ,
,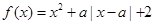
(1)若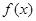 为偶函数,求实数
为偶函数,求实数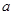 的值;
的值;
(2)记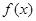 的最小值为
的最小值为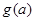 ,求
,求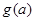 的表达式.
的表达式.
某工厂生产一种产品的原材料费为每件40元,若用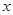 表示该厂生产这种产品的总件数,则电
表示该厂生产这种产品的总件数,则电
力与机器保养等费用为每件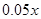 元,又该厂职工工资固定支出12500元。
元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费 (元)表示成产品件数
(元)表示成产品件数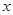 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量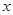 不超过3000件,且产品能全部销售,根据市场调查:每件产品的
不超过3000件,且产品能全部销售,根据市场调查:每件产品的
销售价 与产品件数
与产品件数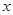 有如下关系:
有如下关系: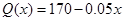 ,试问生产多少件产品,总利润最高?总利润
,试问生产多少件产品,总利润最高?总利润
最高为多少?(总利润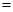 总销售额
总销售额 总成本)
总成本)
已知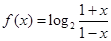
(1)判断 奇偶性并证明;
奇偶性并证明;
(2)判断 单调性并用单调性定义证明;
单调性并用单调性定义证明;
(3)若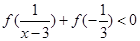 ,求实数
,求实数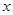 的取值范围.
的取值范围.