设函数
 为奇函数,其图象在x=1处的切线与直线
为奇函数,其图象在x=1处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为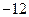 .
.
(I)求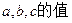 ;
;
(II)求函数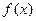 的单调递增区间,并求函数
的单调递增区间,并求函数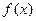 在
在 上的最大值和最小值.
上的最大值和最小值.
已知函数 ,且
,且 的解集为
的解集为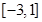 .
.
(1)求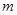 的值;
的值;
(2)已知 都是正数,且
都是正数,且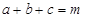 ,求证:
,求证: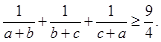
在平面直角坐标系中,以坐标原点为极点,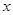 轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为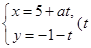 为参数),圆
为参数),圆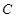 的极坐标方程为
的极坐标方程为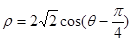 .
.
(1)若圆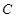 关于直线
关于直线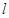 对称,求
对称,求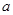 的值;
的值;
(2)若圆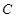 与直线
与直线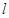 相切,求
相切,求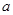 的值.
的值.
二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e=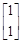 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .
.
(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量.
已知函数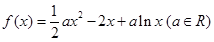
(1)若函数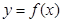 存在极大值和极小值,求
存在极大值和极小值,求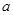 的取值范围;
的取值范围;
(2)设 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中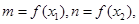 且
且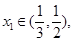 求
求 的取值范围.
的取值范围.
已知双曲线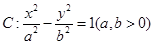 的一条渐近线方程是
的一条渐近线方程是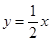 ,它的一个焦点在抛物线
,它的一个焦点在抛物线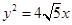 的准线上,点
的准线上,点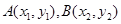 是双曲线
是双曲线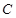 右支上相异两点,且满足
右支上相异两点,且满足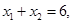
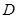 为线段
为线段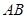 的中点,直线
的中点,直线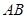 的斜率为
的斜率为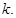
(1)求双曲线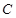 的方程;
的方程;
(2)用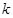 表示点
表示点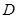 的坐标;
的坐标;
(3)若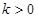 ,
,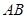 的中垂线交
的中垂线交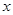 轴于点
轴于点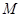 ,直线
,直线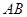 交
交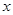 轴于点
轴于点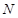 ,求
,求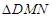 的面积的取值范围.
的面积的取值范围.