如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°. 
(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
如图,四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为梯形,
为梯形, ,
,
 ,且
,且 ,点
,点 是棱
是棱 上的动点.
上的动点.
(Ⅰ)当 ∥平面
∥平面 时,确定点
时,确定点 在棱
在棱 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的余弦值.
的余弦值.
在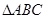 中,
中,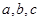 分别为角
分别为角
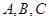 所对的边,且
所对的边,且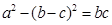 ,
,
(Ⅰ)求角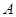 ;
;
(Ⅱ)若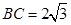 ,
,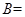
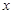 ,
,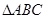 的周长为
的周长为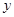 ,求函数
,求函数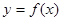 的取值范围
的取值范围
设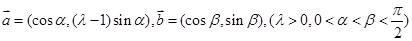 是平面上的两个向量,若向量
是平面上的两个向量,若向量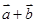 与
与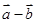 互相垂直.
互相垂直.
(Ⅰ)求实数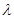 的值;
的值;
(Ⅱ)若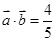 ,且
,且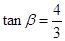 ,求
,求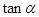 的值.
的值.
已知数列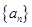 的前
的前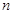 项和为
项和为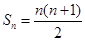 .
.
(Ⅰ)求数列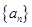 的通项公式
的通项公式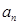 ;
;
(Ⅱ)记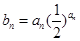 ,求数列
,求数列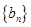 的前
的前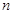 项和
项和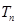
如图,两矩形ABCD,ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.