在等差数列
和等比数列
中，
，
，
是前
项和．
（1）若
，求实数
的值；
（2）是否存在正整数，使得数列的所有项都在数列
中？若存在，求出所有的，若不存在，说明理由；
（3）是否存在正实数，使得数列
中至少有三项在数列
中，但中的项不都在数列中？若存在，求出一个可能的的值，若不存在，请说明理由．
如图，已知四棱锥P—ABCD，底面ABCD为菱形，PA
平面ABCD，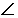
ABC=60O，E，F分别是BC，PC
的中点。H为PD上的动点，EH与平面PAD所成最大角的正切值为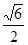
。
（1）证明：AEPD；
（2）求异面直线PB与AC所成的角的余弦值；
（3）若AB=2，求三棱锥P—AEF的体积。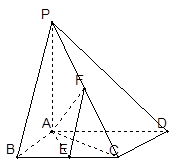
质点A位于数轴x=0处，质点B位于x=2处．这两个质点每隔1秒钟都向左或向右平移一个单位，设向左移动的概率为，向右移动的概率为.（I）求3秒后，质点A在点x=1处的概率；
（II）求2秒后，质点A、B同时在x=2处的概率．
已知
函数y=sinωx•cosωx(ω>0) (ω>0)的周期为 ,
（I） 求ω 的值；
（II） 当0≤x≤时，求函数的最大值和最小值及相应的x的值．
长方体中有公共顶点的三个侧面的面积分别为
，
，
，试求它的外接球的表面积和体积。
如图：在底面为直角梯形的四棱锥P—ABCD中，AD//BC，ÐABC=900，PD^平面ABCD，AD=1，AB=
，BC=4。
[1]、求证：BD^PC；
[2]、求直线AB与平面PDC所成的角；