已知椭圆C：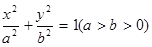
的离心率为
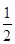，左、右焦点分别为
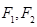，点G在椭圆C上，且
，
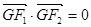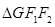的面积为3.
（1）求椭圆C的方程：
（2）设椭圆的左、右顶点为A，B，过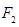
的直线
与椭圆交于不同的两点M，N（不同于点A，B），探索直线AM，BN的交点能否在一条垂直于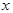
轴的定直线上，若能，求出这条定直线的方程；若不能，请说明理由．
已知函数f(x)=
ax3－bx2 +(2－b)x+1，在x=x2处取得极大值，在x=x2处取得极小值，且0＜x1＜1＜x2＜2。
（1）证明：a＞0；
（2）若z=a+2b，求z的取值范围。
二次函数f(x)=ax2+x+1(a＞0)的图象与x轴的两个不同的交点的横坐标分别为x1、x2。
（1）证明：(1+x1)(1+x2)=1；
（2）证明：x1＜－1，x2＜－1；
（3）若函数y=xf(x)在区间（－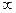
，－4）
上单调递增，试求a的取值范围。
已知0＜a＜1，0＜b＜1，0＜c＜1。求证：(1－a)b，(1－b)c，(1－c)a中至少有一个不大于
。
若a、b、c均为正数，求证：
。
如图，有一块半椭圆形钢板，其长半轴长为2r，短半轴长为r，计划将此钢板割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S。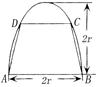
（1）求面积S以x为自变量的函数式，并写出其定义域；
（2）求面积S的最大值。