设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
某养殖厂需定期购买饲料,已知该厂每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价的85%).问:该厂是否应考虑利用此优惠条件?请说明理由.
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤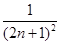 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<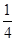 .
.
某镇政府为了更好地服务于农民,派调查组到某村考察.据了解,该村有100户农民,且都从事蔬菜种植,平均每户的年收入为3万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员x(x>0)户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高2x%,而从事蔬菜加工的农民平均每户的年收入将为3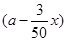 (a>0)万元.
(a>0)万元.
(1)在动员x户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求x的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求a的最大值.
已知0<α< ,β为f(x)=cos
,β为f(x)=cos 的最小正周期,a=
的最小正周期,a= ,b=(cos α,2),且a·b=m,求
,b=(cos α,2),且a·b=m,求 的值.2cos2α+sin 2α+βcos α-sin α
的值.2cos2α+sin 2α+βcos α-sin α