如图，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，连接AE，BE.证明：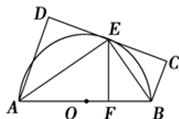
(1)∠FEB＝∠CEB；
(2)EF2＝AD·BC.
设数列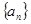
的前
项和为
， 满足
（1）求数列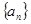的通项公式；
（2）令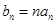
， 求数列
的前项和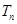
。
在△ABC中，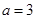
，
，
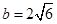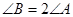
（1）求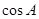
的值；
（2）求
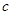的值。
某公司的广告费支出x与销售额y（单位：万元）之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
（1）画出散点图，并判断广告费与销售额是否具有相关关系；
（2）根据表中提供的数据，用最小二乘法求出y与x的回归方程
；
（3）预测销售额为115万元时，大约需要多少万元广告费。
参考公式:回归方程为
其中
， 
为了解某校学生暑期参加体育锻炼的情况，对某班M名学生暑期参加体育锻炼的次数进行了统计，得到如下的频率分布表与直方图：
| 组别 |
锻炼次数 |
频数（人） |
频率 |
| 1 |
 |
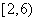2 |
0．04 |
| 2 |
 |
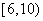11 |
0．22 |
| 3 |
 |
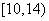16 |
 |
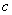| 4 |
 |
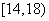15 |
0．30 |
| 5 |
 |
 |
 |
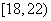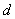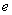| 6 |
 |
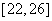2 |
0．04 |
| [ |
合计 |
 |
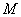1．00 |
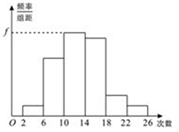
（1）求频率分布表中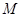
、
、
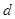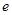及频率分布直方图中
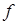的值；
（2）求参加锻炼次数的众数（直接写出答案，不要求计算过程）；
（3）若参加锻炼次数不少于18次为及格，估计这次体育锻炼的及格率。
若不等式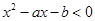
的解集为是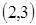
（1）求
，
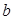的值；
（2）求不等式
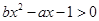的解集。