如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P.
(1)证明:OM·OP=OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.
(本小题满分13分)
已知圆 的圆心为
的圆心为 ,一动圆与这两圆都外切。
,一动圆与这两圆都外切。
(1)求动圆圆心 的轨迹方程;
的轨迹方程;
(2)若过点 的直线
的直线 与(1)中所求轨迹有两个交点
与(1)中所求轨迹有两个交点 、
、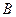 ,求
,求 的取值范
的取值范 围.
围.
(本小题满分12分)
已知函数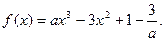
(1)讨论当a > 0时,函数 的单调性;
的单调性;
(2)若曲线 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有
公共点,求实数a的取值范围.
(本小题满分12分)
某批产品成箱包装,每箱4件,一用户在购进该批产品前先取出2箱,再从每箱中任意抽取2件产品进行检验,设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(1)求恰有一件抽检的6件产品中二等品的概率;
(2)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝购买的概率.
(本小题满分12分)
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面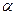 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在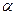 的上侧,分别以△
的上侧,分别以△ 与△
与△ 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(1)求证:PQ⊥BD;
(2)求点P到平面QBD的距离.
(本小题满分12分)
已知函数 ,
,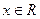 的最大值是1且其图像经
的最大值是1且其图像经 过点
过点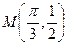 (1)求
(1)求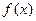 的解析式;
的解析式;
(2)已知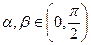 ,且
,且 ,
, 求
求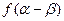 的值.
的值.