某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求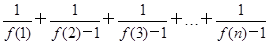 的值.
的值.
(本题12分)一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4,一个质地均匀的骰子(正方体)的六个面上分别标示数字1、2、3、4、5、6,先后抛掷一次正四面体和骰子。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
(本题12分)已知P: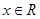 且
且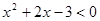 ,已知Q:
,已知Q: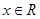 且
且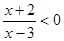 .
.
(Ⅰ)在区间(-4,4)上任取一个实数x,求命题“P且Q”为真的概率;
(Ⅱ)设在数对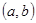 中,
中,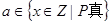 ,
,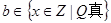 ,求“事件
,求“事件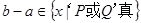 ”发生的概率.
”发生的概率.
(本题10分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)这种抽样方法叫做什么抽样方法?
(Ⅱ)将这两组数据用茎叶图表示出来;
(Ⅲ)将两组数据比较:说明哪个车间的产品较稳定。
(本小题满分12分) 已知二次函数 的图象经过原点,且
的图象经过原点,且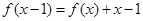 。
。
(1)求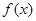 的表达式.
的表达式.
(2)设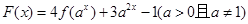 ,当
,当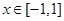 时,
时,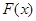 有最大值14,试求
有最大值14,试求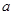 的值.
的值.
(本小题满分12分)已知函数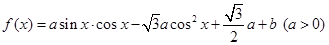
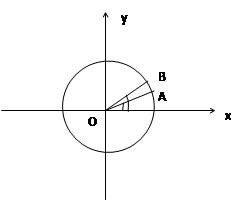
(1)写出函数的最小正周期和对称轴;
(2)设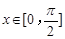 ,
,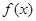 的最小值是
的最小值是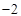 ,最大值是
,最大值是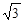 ,求实数
,求实数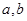 的值.
的值.