如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
下面是用WHILE型语句设计的一个计算S=12+22+…+202的值的一个程序,根据此语句的特点,将其转化为用UNTIL语句书写的程序.
当型(WHILE):
i=1
S=0
WHILE i<=20
S=S+i*i
i=i+1
WEND
PRINT “S=”;S
END
如图是计算1+2+ +3+
+3+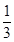 +…+2011+
+…+2011+ 的值的程序框图.
的值的程序框图.
(1)图中空白的判断框内应填________,执行框应填________.
(2)写出与程序框图相对应的程序.
到银行办理个人异地汇款(不超过100万)时,银行要收取一定的手续费.汇款额不超过100元,收取1元手续费;超过100元但不超过5000元,按汇款额的1%收取;超过5000元,一律收取50元手续费.试用条件语句描述汇款额为x元时,银行收取的手续费为y元的过程,画出程序框图并写出程序.
给出如下程序.(其中x满足:0<x<12)
程序: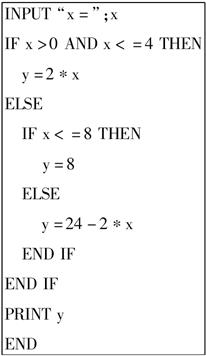
(1)该程序用函数关系式怎样表达.
(2)画出这个程序的程序框图.
输入一个数x,如果它是正数,则输出它;否则不输出.画出解决该问题的程序框图,并写出对应的程序.