为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=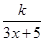 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
已知直线 的方程为3x+4y-12=0,求满足下列条件的直线
的方程为3x+4y-12=0,求满足下列条件的直线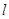 的方程.
的方程.
(1) 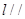
 ,且直线
,且直线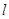 过点(-1,3);
过点(-1,3);
(2) 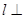
 ,且
,且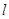 与两坐标轴围成的三角形面积为4.
与两坐标轴围成的三角形面积为4.
已知函数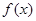 =
= ,其中a≠0.
,其中a≠0.
(1)若对一切x∈R,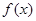 ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数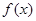 的图像上取定两点
的图像上取定两点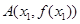 ,
,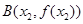
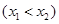 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使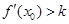 成立?若存在,求
成立?若存在,求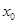 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数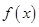 满足
满足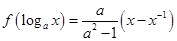 ,其中a>0,a≠1.
,其中a>0,a≠1.
(1)对于函数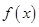 ,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
(2)当x∈(-∞,2)时,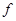
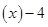 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。
(1)已知函数y=ln(-x2+x-a)的定义域为(-2,3),求实数a的取值范围;
(2)已知函数y=ln(-x2+x-a)在(-2,3)上有意义,求实数a的取值范围.
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系: ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)