已知函数f(x)＝ln x＋
－1.
(1)求函数f(x)的单调区间；
(2)设m∈R，对任意的a∈(－1,1)，总存在x0∈[1，e]，使得不等式ma－f(x0)<0成立，求实数m的取值范围．
如图，正三棱柱
的所有棱长都为2，
为
中点。
（1）求证：
面
；
（2）求二面角
的余弦值；
（3）求点
到平面的距离。
如图，已知三棱锥
的侧棱
两两垂直，且
，
，
是
的中点。
（1）求异面直线
与
所成角的余弦值；
（2）求和平面
所成角的正弦值。
用长为18m的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？
已知函数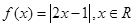
，
（1）解不等式
；
（2）若对于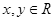
，有
．求证：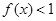
．
在直角坐标系
中，直线
的参数方程为
（t为参数），再以原点为极点，以x正半轴为极轴建立坐标系，并使得它与直角坐标系有相同的长度单位，在该极坐标系中圆C的方程为
．
（1）求圆C的直角坐标方程；
（2）设圆C与直线将于点
、
，若点
的坐标为
，求
的值 ．