已知函数f(x)=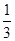 x3+
x3+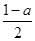 x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
已知二次函数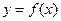 在
在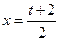 处取得最小值
处取得最小值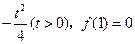 .
.
(1)求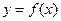 的表达式;
的表达式;
(2)若任意实数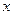 都满足等式
都满足等式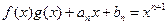 (
(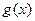 为多项式,
为多项式,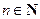 ),试用
),试用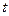 表示
表示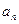 和
和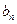 ;
;
(3)设圆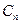 的方程为
的方程为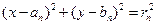 ,圆
,圆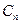 与
与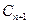 外切
外切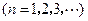 ,
,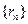 为各项都是正数的等比数列,记
为各项都是正数的等比数列,记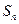 为前
为前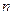 个圆的面积之和,
个圆的面积之和,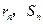 .
.
求过点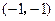 的直线使它与直线
的直线使它与直线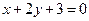 的夹角为
的夹角为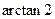 .
.
已知 是长轴为4的椭圆上的三点,点
是长轴为4的椭圆上的三点,点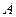 是长轴的一个顶点,
是长轴的一个顶点,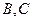 过椭圆中心
过椭圆中心 (如图),且
(如图),且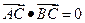 ,
,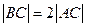
(I)求椭圆的方程;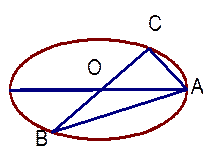 (Ⅱ)如果椭圆上的两点
(Ⅱ)如果椭圆上的两点 ,使
,使 的平分线垂直于
的平分线垂直于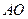 ,是否总存在实数
,是否总存在实数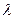 ,使
,使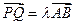 。请给出证明。
。请给出证明。
已知: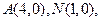 若点
若点 满足
满足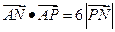 。
。
(I)求点 的轨迹方程,并说明轨迹是什么曲线?
的轨迹方程,并说明轨迹是什么曲线?
(II)求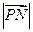 的取值范围;
的取值范围;
(III)若 求
求 上的取值范围。
上的取值范围。
已知椭圆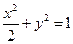 的右准线
的右准线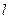 与
与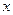 轴相交于点
轴相交于点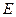 ,过椭圆右焦点
,过椭圆右焦点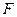 的直线与椭圆相交于
的直线与椭圆相交于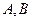 两点,点
两点,点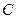 在右准线上,且
在右准线上,且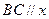 轴。
轴。
求证:直线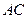 经过线段
经过线段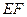 的中点。
的中点。