如图,已知抛物线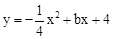 与
与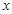 轴相交于A、B两点,与
轴相交于A、B两点,与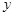 轴相交于点C,若已知B点的坐标为B(8,0).
轴相交于点C,若已知B点的坐标为B(8,0).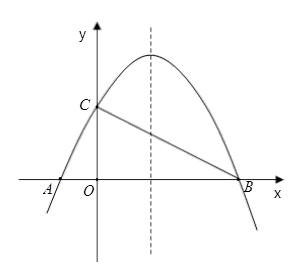
(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥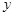 轴,求MN的最大值;
轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
甲乙两单位随机选派相同人数参加科普知识比赛;每人得分成绩只有70分、80分、90分三种结果中一种,已知两单位得80分的人数相同,根据下列统计图回答问题.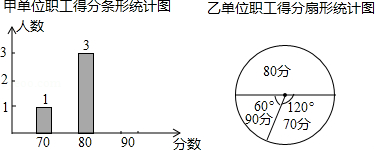
(1)求甲单位得90分的人数,将甲单位职工得分条形统计图补充完整;
(2)分别计算两个单位职工参加比赛成绩的平均分,由此你能估计出哪个单位职工对此次科普知识掌握较好,并说明理由;
(3)现从甲单位得80分和90分的人中任选两个人,列出所有的选取结果,并求两人得分不同的概率(用大写字母代表得90分的人,小写字母代表得80分的人).
已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.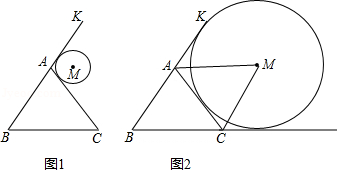
将一根长为16 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为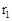 和
和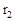 .
.
(1)求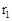 与
与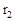 的关系式,并写出
的关系式,并写出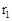 的取值范围;
的取值范围;
(2)将两圆的面积和S表示成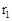 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.
若一次数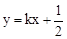 和反比例函数
和反比例函数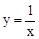 的图象都经过点C(1,1).
的图象都经过点C(1,1).
(1)求一次函数的表达式;
(2)已知点A在第三象限,且同时在两个函数图象上,求点A的坐标.
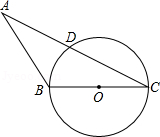
如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.
(1)求∠ACB的大小;
(2)求点A到直线BC的距离.