已知抛物线 经过
经过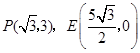 及原点
及原点 .
.求抛物线的解析式.
过
 点作平行于
点作平行于 轴的直线
轴的直线 交
交 轴于
轴于 点,在抛物线对称轴右侧且位于直线
点,在抛物线对称轴右侧且位于直线 下方的抛物线上,任取一点
下方的抛物线上,任取一点 ,过点
,过点 作直线
作直线 平行于
平行于 轴交
轴交 轴于
轴于 点,交直线
点,交直线 于
于 点,直线
点,直线 与直线
与直线 及两坐标轴围成矩形
及两坐标轴围成矩形 (如图).是否存在点
(如图).是否存在点 ,使得
,使得 与
与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,请说明理由
点的坐标;若不存在,请说明理由如果符合(2)中的
 点在
点在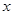 轴的上方,连结
轴的上方,连结 ,矩形
,矩形 内的四个三角形
内的四个三角形 之间存在怎样的关系?为什么?
之间存在怎样的关系?为什么?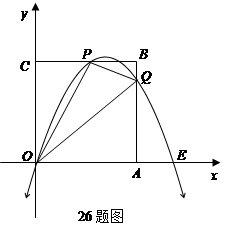
已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+
S△PCD理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵ S△PBC+S△PAD=BC·PF+AD·PE=BC(PF+PE)=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD.
∴ S△PBC=S△PAC+S△PCD.
请你参考上述信息,当点P分别在图2、图3中的位置时,S△PBC、S△PAC、S△PCD又
有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给
予证明.
某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
| A |
B |
|
| 成本(万元/套) |
25 |
28 |
| 售价(万元/套) |
30 |
34 |
该公司对这两种户型住房有哪几种建房方案?
该公司如何建房获得利润最大?
根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会
提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得
利润最大?注:利润=售价-成本
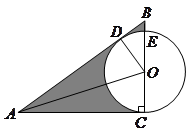
如图, 中,
中,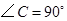 ,
,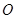 为直角边
为直角边 上一点,以
上一点,以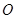 为圆心,
为圆心, 为半径的圆恰好与斜边
为半径的圆恰好与斜边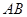 相切于点
相切于点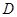 ,与
,与 交于另一点
交于另一点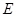 .
.求证:
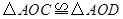
若
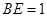 ,
, ,求圆O的半径及图中阴影部分的面积
,求圆O的半径及图中阴影部分的面积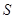 .
.
初中生对待学习的态度一直是教育工作者 关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题: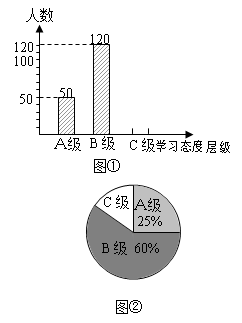
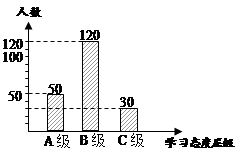
此次抽样调查中,共调查了名学生;
将图①补充完整;
求出图②中C级所占的圆心角的度数
根据抽样调查结果,请你估计该区近20000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?