某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、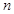 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.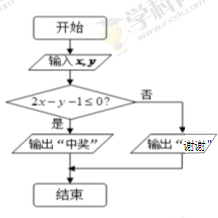
(1)求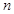 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为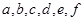 ,现随机从中抽取2人上台抽奖,
,现随机从中抽取2人上台抽奖,
求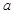 和
和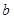 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个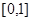 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
已知 ,q:x2-4x+4-9m2≤0 (m>0),若
,q:x2-4x+4-9m2≤0 (m>0),若 p是
p是 q的充分而不必要条件,求实数m的取值范围.
q的充分而不必要条件,求实数m的取值范围.
设函数 且
且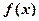 的图象在
的图象在 轴右侧的第一个最高点的横坐标为2。
轴右侧的第一个最高点的横坐标为2。
(1)求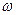 ;
;
(2)若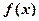 在区间[8,16]上的最大值为3,求m的值。
在区间[8,16]上的最大值为3,求m的值。
设三次函数h(x)=px3+qx2+rx+s满足下列条件:h(1)="1,h(-1)=" -1,在区间(-1,1)上分别取得极大值1和极小值-1,对应的极点分别为a,b。
(1)证明:a+b=0
(2)求h(x)的表达式
(3)已知三次函数f(x)=ax3+bx2+cx+d在(-1,1)上满足-1<f(x)<1。证明当|x|>1时,有|f(x)|<|h(x)|
如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
C过F的切线交于点P和点Q,则P、Q必在以F为焦点,l为准线的同一条抛物线上.
(Ⅰ)建立适当的坐标系,求出该抛物线的方程;
(Ⅱ)对以上结论的反向思考可以得到另一个命题:
“若过抛物线焦点F的直线与抛物线交于P、Q两点,
则以PQ为直径的圆一定与抛物线的准线l相切”请
问:此命题是否正确?试证明你的判断;
(Ⅲ)请选择椭圆或双曲线之一类比(Ⅱ)写出相应的命题并
证明其真假.(只选择一种曲线解答即可,若两种都选,则以第一选择为评分依据)
政府决定用“对社会的有效贡献率”对企业进行评价,用 表示某企业第n年投入的治理污染的环保费用,用
表示某企业第n年投入的治理污染的环保费用,用 表示该企业第n年的产值. 设
表示该企业第n年的产值. 设 (万元)且以后治理污染的环保费用每年比上一年增加2
(万元)且以后治理污染的环保费用每年比上一年增加2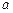 (万元);又设
(万元);又设 (万元),且企业的产值每年比上一年的平均增长率为10%. 用
(万元),且企业的产值每年比上一年的平均增长率为10%. 用 表示企业第n年 “对社会的有效贡献率”
表示企业第n年 “对社会的有效贡献率”
(Ⅰ)求该企业第一年和第二年的“对社会的有效贡献率”;
(Ⅱ)已知1.13≈1.33,1.18≈2.14,试问:从第几年起该企业“对社会的有效贡献率”不低于20%?