设 ,
,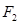 分别是椭圆
分别是椭圆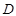 :
: 的左、右焦点,过
的左、右焦点,过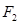 作倾斜角为
作倾斜角为 的直线交椭圆
的直线交椭圆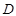 于
于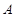 ,
,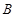 两点,
两点,  到直线
到直线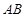 的距离为
的距离为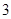 ,连结椭圆
,连结椭圆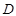 的四个顶点得到的菱形面积为
的四个顶点得到的菱形面积为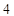 .
.
(1)求椭圆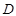 的方程;
的方程;
(2)过椭圆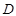 的左顶点
的左顶点 作直线
作直线 交椭圆
交椭圆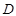 于另一点
于另一点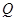 , 若点
, 若点 是线段
是线段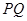 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足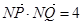 ,求实数
,求实数 的值.
的值.
已知直线
(
为参数),
(
为参数),
(Ⅰ)当
时,求
与
的交点坐标;
(Ⅱ)过坐标原点
做
的垂线,垂足为
,
为
中点,当
变化时,求
点的轨迹的参数方程,并指出它是什么曲线.
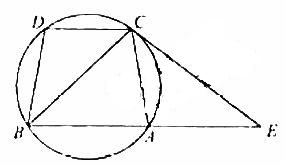
如图,已经圆上的弧
,过
点的圆切线与
的延长线交于
点,证明:
(Ⅰ)
;
(Ⅱ)
.
设函数
。
(1)若
,求
的单调区间;
(2)若当
时
,求
的取值范围.
设
分别是椭圆
的左、右焦点,过
(1)求
(2)设点
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:

(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由.
附:
