有一个二次函数的图象,三位学生分别说出了它的一些特点.
甲:对称轴是直线x=4;
乙:与x轴两交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3;
请写出满足上述全部特点的二次函数解析式:
已知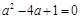 ,求代数式
,求代数式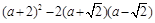 的值.
的值.
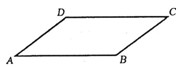
如图,已知平行四边形 .
.
(1)用直尺和圆规作出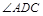 的平分线
的平分线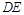 ,交
,交 于点
于点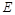 ,(保留作图痕迹,不要求写作法)(2)求证:
,(保留作图痕迹,不要求写作法)(2)求证: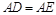 .
.
解不等式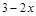 ≤
≤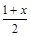 .
.
如图,面积为39的直角梯形OABC的直角顶点C在 轴上,点C坐标为
轴上,点C坐标为 ,AB=
,AB= ,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在
,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在 轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=
轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE= ,OF=
,OF= .
.
(1)求点D的坐标及 的度数;
的度数;
(2)若点E在 轴正半轴上运动,求
轴正半轴上运动,求 与
与 的函数关系式;
的函数关系式;
(3)在点E的运动过程中,是否存在某一时刻,使得△DEF成为等腰三角形?若存在,请求出所有符合条件的点F的坐标;若不存在,请说明理由.
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图(1).然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个小正方形(阴影部分),假设长方形的长为 ,宽为
,宽为 ,且
,且 .
.
(1)求图(1)中 与
与 的函数关系式;
的函数关系式;
(2)若阴影小正方形边长为1,求图(2)中 与
与 的函数关系式;
的函数关系式;
(3)在图(3)中作出(1)、(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上研究完成下表:
| 图(2)中小正方形边长 |
1 |
2 |
3 |
4 |
… |
 |
6 |
… |
|||
 |
10 |
… |
观察上表,设图(2)中小正方形边长为 ,请分别猜想
,请分别猜想 与
与 、
、 与
与 的关系,并证明你的猜
的关系,并证明你的猜