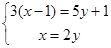如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD. (参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).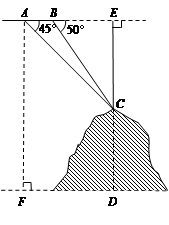
(本题10分)如图,AB是⊙O的直径,PA,PC分别与⊙O 相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E,记∠EPD=∠1,∠EDO=∠2.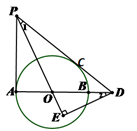
(1)求证:∠1=∠2;
(2)若PC=6,tan∠PDA=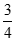 ,求OE的长。
,求OE的长。
(本题10分)如图,某校综合实践活动小组的同学欲测量公园内一棵树 的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端
的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端 的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端
的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端 的仰角为60°.已知点A 的高度AB为
的仰角为60°.已知点A 的高度AB为 ,台阶AC的坡度为
,台阶AC的坡度为 (即
(即 ),且
),且 、
、 、
、 三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°
三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65° 2.1,cos65°
2.1,cos65° 0.4, sin35°
0.4, sin35° 0.6,tan35°
0.6,tan35° 0.7,
0.7, 1.7,结果保留一位小数).
1.7,结果保留一位小数).
(本题8分)如图,在□ABCD中,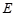 、
、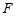 是
是 、
、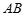 的中点,
的中点,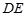 、
、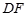 的延长线分别交
的延长线分别交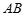 、
、 的延长线于
的延长线于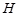 、
、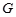 ;
;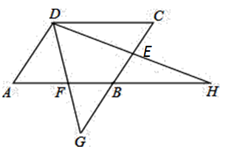
(1)求证:BH=AB;
(2)若四边形 为菱形,试判断
为菱形,试判断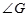 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
(本题8分)如图,在10×6的正方形网格中,每个小正方形的边长均为1,线段AB的端点A、B均在格点上.分别在图甲和图乙中作出以AB为一腰的等腰△ABC,使其顶角分别为直角和钝角,点C在格点上,并直接写出△ABC的周长。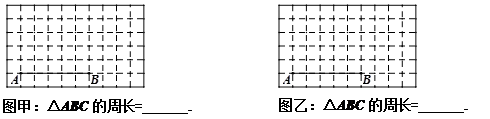
(本题10分,每小题5分)
(1)计算: 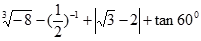 ;
;
(2)解方程组: