设函数f(x)= (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
(本小题满分13分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率 ,例如:
,例如: .
.
(1)求 ;
;
(2)求第 个月的当月利润率
个月的当月利润率 ;
;
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
(本小题满分13分)设数列 是公比大于1的等比数列,
是公比大于1的等比数列, 为其前
为其前 项和,已知
项和,已知 =7且
=7且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列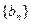 的前
的前 项和
项和 
(3)求 的表达式.
的表达式.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面 ;
;
(2)当 且E为PB的中点时,
且E为PB的中点时,
求AE与平面PDB所成的角的大小.
(本小题满分12分)袋子中有质地、大小完全相同的4个球,编号分别为1,2,3,4.甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,若两个编号的和为奇数算甲赢,否则算乙赢.记基本事件为 ,其中
,其中 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。
(1)列举出所有的基本事件,并求甲赢且编号的和为5的事件发生的概率;
(2)比较甲胜的概率与乙胜的概率,并说明这种游戏规则是否公平。(无详细解答过程,不给分)
(3)如果请你猜这两球的号码之和,猜中有奖.猜什么数获奖的可能性大?说明理由.
(本小题满分12分)在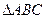 中,已知
中,已知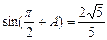 .
. (1) 求
(1) 求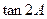 的值;
的值; (2) 若
(2) 若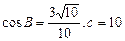 ,求
,求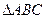 的面积.
的面积.